law of cosines

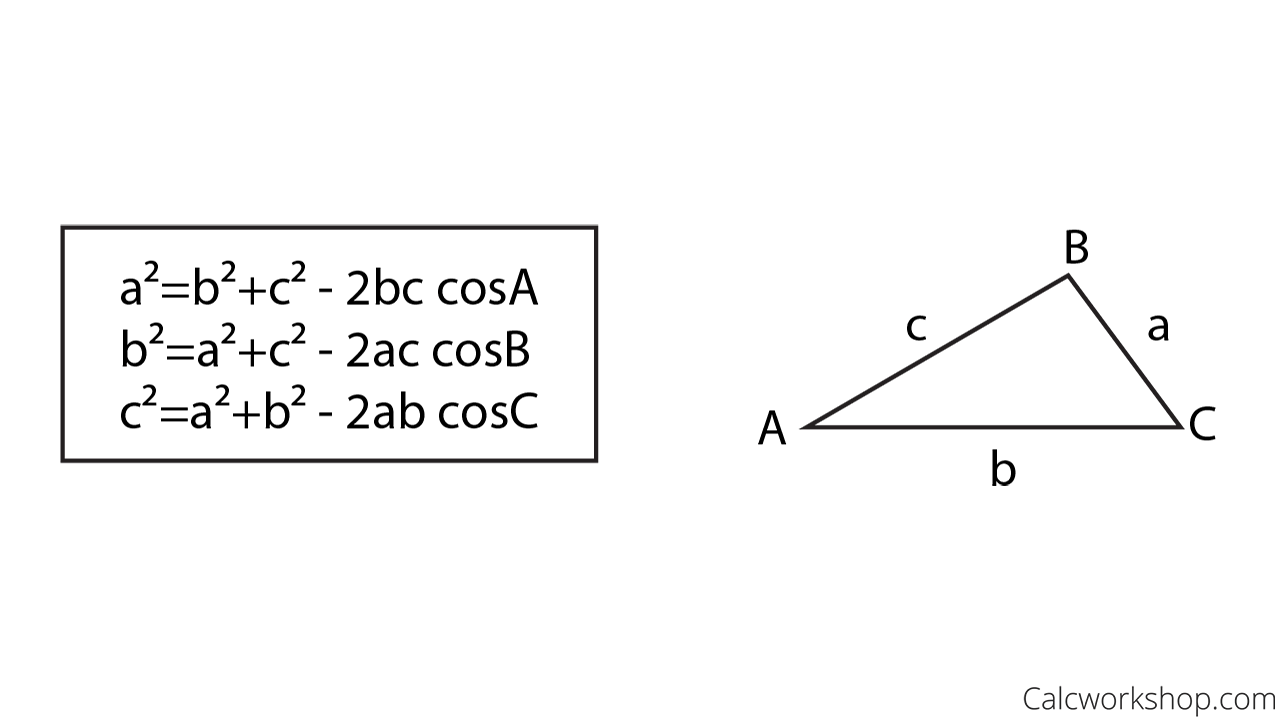
**Why the Law of Cosines Is Surprisingly Relevant in U.S. Education and Beyond** Have you ever glanced at a map, measured a roof angle, or tried to calculate the shortest path between two non-straight points—and paused, wondering why the formula isn’t taught earlier? The law of cosines, a staple of triangle geometry, is quietly gaining attention across U.S. educational platforms and practical applications. While often associated with advanced math, this foundational principle is becoming more visible in digital learning spaces, especially as students and professionals seek deeper understanding of spatial relationships. Exploring *why* it’s a hot topic now reveals broader trends in STEM literacy, practical problem-solving, and the growing demand for intuitive math comprehension. With more emphasis on real-world math applications, the law of cosines is emerging as a vital tool—not just for trigonometry exams, but for architecture, navigation, law enforcement mapping, and even outdoor recreation. As learners and professionals seek reliable, non-clunky explanations, digital content on this topic is rising in visibility, particularly on cloud-based search platforms like Amazon Discover, where clarity and relevance matter most. **How the Law of Cosines Actually Works** The law of cosines connects the lengths of the sides of any triangle to the cosine of one of its angles. For a triangle with known sides *a* and *b* and the included angle *C*, the formula calculates the length of side *c* opposite angle *C* using: c² = a² + b² – 2ab·cos(C)

**Common Questions About the Law of Cosines** **How is the law of cosines used in real life?** Beyond classrooms, professionals apply the law of cosines to calculate survey lines, determine distances in GPS navigation, assess structural stability in construction, and even optimize solar panel angles for maximum efficiency. Its ability to resolve angles and distances in non-right triangles makes it indispensable in spatial planning. **Why do so many people initially struggle with it?** Common confusion stems from mixing it up with the Pythagorean theorem, which only applies to right-angled triangles. The inclusion of cosine introduces a layer of trigonometric reasoning users must adapt to—especially when angles aren’t labeled or measured with precision. **Who Benefits from Learning the Law of Cosines?** Students preparing for advanced math or STEM fields rely on it for physics, engineering, and computer graphics. Professionals in architecture, civil planning, and geospatial analysis use it daily to ensure accuracy. Even hikers, DIYers, and creators using mapping apps silently benefit from its logic in calculating safe routes or angles outdoors. **What Do People Often Get Wrong?** Myth: Only advanced math majors need the law of cosines. Reality: It’s a foundational tool for many applied fields, and understanding it early builds intuitive problem-solving skills. Myth: The cosine term makes it too complex. Reality: When applied correctly, it’s a precise and efficient solution—far more accurate than approximations in non-right triangles. **Applications Across Industries and Everyday Life** In architecture, it helps visualize roof slopes and load distribution in irregular designs. Law enforcement and rescue teams use it to map incident sites and compute optimal paths.